By: Kris Young and Dan Li
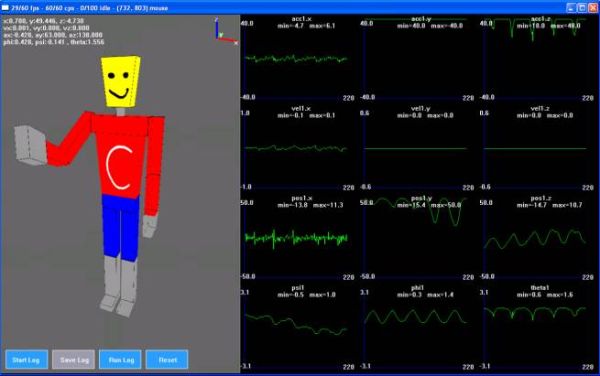
See the results section for movie clips of the motion capture system in action.
Abstract
Human-Computer interface may perhaps be both the most limiting and liberating aspect of humans working with computers.It can, for instance, limit the input complexity to the system or may, alternatively, provide a great range of options.Imagine the possibilities of a hard-wired user interface, in which computers not just necessarily desktop PCs, but computers anywhere observe and react to the movements of their human counterparts. Surely there is a wealth of possibilities yet to be explored.
Complex and very expensive systems have been developed to model the movement of a human.Applications of such motion capture systems can be seen in the movie industry and animation, biomechanics, ergonomics and human-computer interaction. Most of these systems range into the tens to hundreds of thousands of dollars.
Introduction
We are attempting to create a motion capture system using accelerometers that allows for large scalability and a dynamic range of purposes that is affordable to the every day user. Modern MEMs accelerometers have the ability to measure both the Earths gravitational acceleration, as well as dynamic acceleration of the movement of the sensor within the device. Using these devices, we have attempted to design an inexpensive, accurate and scalable the number of measurable points system. We developed a system that can model any two-joint portion of the human body given a set of initial conditions of the movement of both joints. Using the serial port as a communications link, we were able to reproduce the bodys movements and orientation using a graphics package called GameX.
High Level Design
Theory Of Operatio
We used our microcontroller to sample and average our accelerometers attached to the body. The data is then transmitted serially to a windows-PC where the data is reconstructed and displayed to the user in real-time.
Motion Capture Math
Overview:
Motion can be captured using several different methods. The two main methods used to extract motion for this project are exploitation of the g-field to observe sensor orientation, and numerical integration to extract change in position. These two options are explored further in the next few sections. First, we will discuss problems to overcome, followed by potential solutions.
In general, the human body has several properties that help constrain motion and help reconstruction of motion from acceleration. Notice that most motion about a joint is rotational. This greatly restricts problems in reconstructing movement because knowledge of how a particular point of the body will move is dependent on the motion type of that points parent joint.Moreover, the length of a limb in constant, thus giving a constant radius of movement between joints.
Much of this theory is from reference [a1].
For general purposes, we will define the coordinate system for motion capture as follows:
The Z-Axis will be the up-down axis, which is parallel to the earths gravitational field.
The Y-Axis will be facing out from the front of the person.
The X-Axis will be facing out from the side of the person.
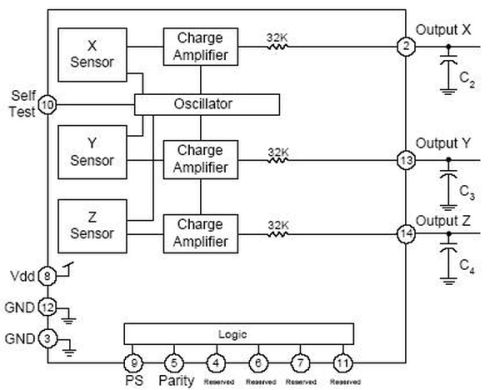
In the case that the KXM52 is parallel to the Cartesian plane, direct observation of the three outputs (X, Y and Z) will directly reflect the acceleration observed in that direction.
The Dynamic Axis Problem:
One problem with human motion is it is highly non-planar. The result is movement of the accelerometer axes with respect to the motion capture coordinate system. Using 3D-cartesian coordinates in changing axes of measurement can create many undesirable problems. First, if the g-field is considered fixed, a moved axis will pick up accelerations due to g that are not filtered out. Secondly, motion in the moved axis wont directly represent motion for that point correctly.
Consider the case of an accelerometer measuring acceleration in three orthogonal planes. If the sensor is initially attached to the top of a hand, then the g-field is measured only in the z-axis. Now, if the hand is rotated upwards, a portion of the g-field is observed in both the y and z-axis. If the hand is allowed to rotate 90 degrees, then a portion of the g-field is then observed in both the x and z-axes. These changes will result in a moving gravity vector, as well as dynamic acceleration vectors.
G-Field Observation (Orientation Tracking) Method:
Recall that the KXM52 tri-axis accelerometers used for this project detects both static accelerations, such as the acceleration due to gravity (g) and accelerations due to motion (a).This method makes the assumption that any quick (short-term) acceleration may be disregarded and only DC-accelerations, such as the constant g-field should be observed. This is a relatively valid assumption as the output of the accelerometer is bandwidth limited with a 3dB cutoff frequency of 50Hz.
The orientation of the KXM52 can be uniquely constructed by observing the g-field offset in each axis. If motion in any z-plane is being constructed, then the angle from the normal can be decided.
In general, we define three angles in our coordinate system to help with the dynamic movement of axes:
The Normal is defined as the z-axis.
Theta is defined as the angle of the g-field in the xz plane, with respect to the normal.
Phi is defined as the angle of the g-field in the yz plane, with respect to the normal.
Psi is defined as the angle rotation angle of the point in the xy (Cartesian) plane.
These definitions are shown below in Figure (2).
We can find these angles using simple trigonometry, as shown below in equation (1).
Using the function atan2(y, x ) in c++ will compute the arctan of y/x in the output range of p to p [radians]. Thus, human rotational motion can be completely reconstructed because no joints in the body exhibit greater than 360-degree planar rotation about a single point.
Numerical Integration Method:
In cases where there is no G-vector to measure (notably, when the axis of motion is perpendicular to the earths gravity vector), one must employ the equations of motion to extract positional changes.
Recall the equations of motion shown below in (2).
Equation (2): Equations of Motion
Using the Euler method, these equations can be approximated by equation (3):
Equation (3): Euler Approximation of Equations of Motion
Taking the small time change (dt) being the sample rate, reduces the equations (in c++ code) to:
Equation (4): C++ Implementation of Euler Approximation of Equations of Motion
v += a;
s += v;
Although this method may seem easier than orientation tracking upon first pass, it is actually substantially more complicated. In this method, the Dynamic Axis Problem is present. Additionally, signal noise will cause substantial jitter to these systems of equations. Because this algorithm computes a running numerical integration, the noise will become additive and can take control of the system entirely. Thus, it is important to develop a filtering system to reduce the noise and allow for proper observation of movement. The next few sections describe our theoretical approach to solve this complicated problem.
Signal Filtering:
An obvious consequence of using long wires and finite precision equipment with limited sampling frequency is noise and error. With respect to numerical integration, finite signal resolution and signal noise can all but destroy a signals usefulness. To combat this problem for the numerical integration method, the signals are filtered and band-limited to give more desirable results. The effect can be quite dramatic results. Take for example, the rotational motion of ones wrist, left and right perpendicular to the earths gravitational vector. Obviously, the G-observation method is useless in this case. In figure (3) below, the raw acceleration data is shown as the green plot.
Notice the jitter (quantization error and signal noise) that is inherit to the raw acceleration data. Using a moving average lowpass filter can help destroy much of this noise. Averaging the last N samples together and dividing by N implements such a filter. Expressed in terms of a difference equation, this is:
Equation (5): Moving Average Filter Difference Equation
The result is the blue plot shown above. Notice that there is a small time shift on the output as a result of this filter, while noise immunity is much higher.
Another consequence of both filtering and signal noise is uneven areas for the concave up and concave down humps in the blue waveform. The result, seen through numerical integration of the signal as they velocity (red) plot, is an undesirable DC offset known as drift error. While performing a second numerical integration to extract position (the black plot), the value will drift off to positive or negative infinity. To correct this problem, a small damping term is added into the velocity computation:
1. If the average acceleration is in the range [-.4, .4]
2. Damp the signal by: v = .1*v
Notice how the velocity waveform behaves somewhat appropriately over the range of acceleration, but with some drift term left at the end. The drift is eliminated almost instantly as a result of the damping, once the acceleration settles down. The result on the position plot is a change in position, followed by a constant position.
DC Filtering [f1]:
A final technique required to run our motion capture algorithm requires the DC-filtering of some signals (namely, of a gravity term when necessary). This is implemented using the difference equation:
Equation (6): DC Filtering Difference Equation
With Z-Transform:
Equation (7): Transfer Function of DC Filter
Where R is any constant in the range 0 to 1 (depending on the sampling frequency). The plot below shows the frequency response of the DC Blocking filter, choosing R to be .1.
For more detail: A Motion Capture System Using Accelerometers