In some cooking scenarios, it is desirable to achieve a specific object temperature and keep the object at that temperature. However, it is difficult to maintain a constant temperature without constant attention. To aid cooking in this scenario, we created a device that can be added to an electric stovetop or hot plate and serve as an automated assistant.
High Level Design top
The broad goals of our project were:
- measurement and control of a cooking device
- automated cooking of certain food types.
Accomplishing these goals would make the device useful for home cooking where it is difficult to keep object at desired temperature without constant attention. An early decision was made to not modify a cooking device, but rather physically manipulate the dial. This choice avoided safety problems with modifying electrical appliances and made our project easy to implement in existing cooking systems. All of our testing was done on a single electric burner, but the project could be easily used on other electric burners. It has not been designed to work with gas burners which require lighting.
Once the device is attached to the dial of the electric burner, the desired position must be determined by a controller using temperature measurements. We have built two multi-purpose temperature probes. The first probe uses a temperature sensing integrated circuit (IC) which outputs a voltage proportional to the temperature in the range of -50C to +150C with 0.2C nominal resolution and limited error. The second probe uses a negative-temperature-coefficient (NTC) thermistor and is designed to operate from 0C to +200C with larger absolute error than the IC probe. A custom circuit was designed to precisely read the resistance of the NTC thermistor over the large range of 200ohms to 15000ohms with low current through the thermistor. Simply changing the resistance in series with the thermistor would lead to excessive current that would cause self-heating and damage of the sensor. The mechanical and thermal design of the temperature probes was very challenging. The probes needed to safely and quickly transfer heat from the object to the temperature sensor while not being severely affected by the environment temperature. After considerable amount of design work and one failed probe design, we came up with a probe and probe holder with the following characteristics:
- fast heat from object to sensor
- in presence of environment temperature much lower than object temperature, still has small offset between the object and sensor temperatures
- works for internal meat temperature and water temperature with various sized cookware
- simple and cheap to construct
A proportial-integral-derivate (PID) controller was used to determine where to position the dial given the temperature measurements. Tuning the gains for the controller required a simulation because experiments are very time-consuming in slow thermal systems. The simulation was developed in Matlab and included an approximate thermal model of heating up water with a PID controller that changed the heat input to the system. Many, many thermal parameters needed to be approximated, the details of which can be seen in the Matlab files available here. The thermal simulation used after common equations and simplifications.
Before the simulation can be conducted, the heat input from the electric burner must be found as a function of the dial position (set by the controller). Based on a 1.1kW peak electrical power rating of our hot plate, we assumed the maximum heat input to be 750W. We then assumed the heat input from the electric burner was linear with respect to the dial position. This assumption causes large inaccuracies in the predicted heat input, but it avoid us making a model of the electric burner that is both complicated and specific to the electric burner we purchased. During testing, not knowing the true heat input from the hot plate adversely affected the controller but the project still remained functional. Output calculation in the controller implementation on the MCU was done as a ratio of the maximum heat input. By modifying the QMAX symbol, the controller should scale properly. Output calculation also took into account the point at which the dial turns on. On our hot plate, the device is not on between “OFF” and “LOW.” Therefore, we needed to add an offset to the controller output based on the latest calibration result of the minimum on state of the hot plate. The software section details these aspects, but these considerations do affect both the performance of the controller and the applicability of our project to other electric burners.
Newton’s law of cooling is used to find the heat loss to the environment, Qcool by assuming reasonable values for parameters.
qcool(i) = hair*SAobj*(Tbot(i-1) – Tenv)
where:
hair = approximate heat transfer coefficient of air
SAobj = surface area of container holding water
Tenv = ambient temperature in a hot kitchen
Tobj = temperature of the water
Then, the change in object temperature is calculated based on the net heat input
delT = dt*(qin(i)-qcool(i))/(mobj*cobj);
Tbot(i) = Tbot(i-1) + delT;
where:
mobj = mass of the water
cobj = specific heat capacity of water
qin = heat input from the hot plate
This simulation was run for various water depths (which changes heat capacity) and controller gains. Ultimately, gains were selected to produce an overdamped response since we don’t want the controller to overshoot the desired temperature as that may burn the food. The results showed that derivative control had negligible effect and that during normal heating the control should saturate in the beginning, corresponding to “HI” on the hot plate.
Hardware top
Overview
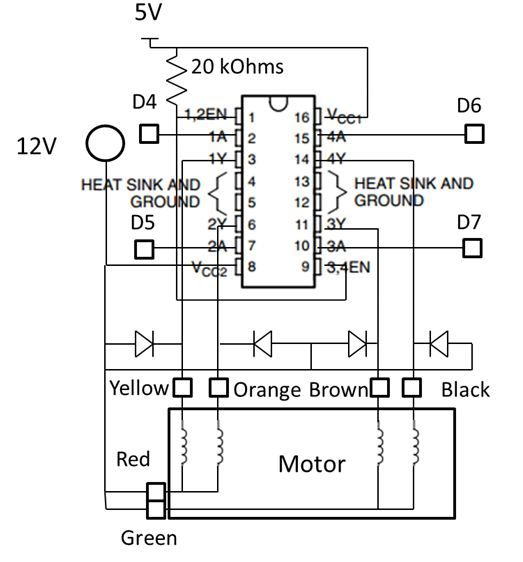
The hardware setup of this project consists of a heating device (an electric hot plate in our case) of which control knob is to be attached to a stepper motor, 2 interchangeable temperature measuring probes, and control and interfacing circuitry.
The electronic hardware was designed with modularity and ease of testing in mind. A single ATMega644 MCU on a target board interfaces with a number of physically separate peripheral devices of different yet essential functions. Circuitry on the measurement board adjusts and interfaces the temperature probe outputs with the MCU. The stepper motor control circuit board controls and powers the stepper motor that is used to control the heating device. A 4×4 keypad and 4 lines x 20 character LCD screen allows the user to interact with the controller.
Whenever we discuss a single piece of hardware, such as a temperature measurement board, it is physically separate in our setup from other devices and connected only via a detachable harness (as shown in pictures). Detachable harnessing allowed us to remove any component at any time and debug it separately from the rest of the circuit.
Probes
Due to our concern with reliability, accuracy, and absolute ratings, we had decided to build two different measurement probes. One (the IC probe) is based on a AD22100 analog voltage output sensor. This sensor provides an accurate (+-2%) and a very linear analog voltage output with a temperature range of -50C to 150C. The package contains three leads – +5V supply voltage, 0V ground, and analog output – which are connected by long wires to the measurement board. The sensed temperature can be easily calculated from the voltage output by a simple equation:
T = (VOUT*(5V/V+)-1.375V)/( 22.5 mV/�C)
The second probe (NTC probe) utilizes a NTC thermistor that provides a resistance across its two leads as a decreasing exponential function of the sensed temperature. While the thermistor might provide a measurement that is not as absolutely accurate (), and harder to measure due to the additional analog circuitry necessary to deal with its non-linearity, it has a much wider temperature range (). The following equation relates the resistance across the NTC thermistor and the temperature:
rNTC = Ro*exp(B*(1/T – 1/To));
Ro, B, and To are nominal values of a specific thermistor that one can find in a datasheet.
The probe design proved to be challenging as we were looking for the best and most immediate heat transfer medium between the food/water and the sensor. We first attempted to glue the sensors to a thin piece of solid aluminum (Figure 3). This, however, introduced an unacceptable delay and level heat loss in the probe. We finally decided to use hollow aluminum knitting needles that are wide enough to hold a sensor and its wires and have a narrowing shape towards the bottom, perfect for insertion into heartier food. After cutting the top of a needle, vegetable (i.e. soybean) oil was poured into the needles to submerge the sensors with a heat conducive but electrically isolating material. The probe was then sealed on top with hot glue. As it will be discussed in the results section, this design provided the best heat transfer characteristics out of considered probes.
Measuring Circuit
The main purpose of the measuring circuit is to condition the analog signals coming from the temperature probes so that can be accurately measured by the MCU ADCs. The circuit was built on a separate board providing a certain level of isolation of the supply and signal lines from the rest of the project circuitry.
Because the IC sensor already provides a linear output that is in the input range of the ADCs, the only circuit elements between the probe output and ADC input is a low pass filter to get rid of higher frequency noise.
However, the NTC sensor circuit requires a little more circuitry in order to amend for its non-linear behavior at higher temperatures. First of all, in order to measure the resistance of the sensor, the sensor is attached to a series resistor (Rs) pulled Vcc high on one end and grounded on the other, creating a voltage divider. The selection of Rs was based on several factors. If Rs is too small, the NTC will dissipate too much power, which may cause damage or cause a self-heating bias in the temperature measurement. However, large values of Rs will cause very small voltages across the NTC. We selected 5kOhms for the series resistor as this limits power dissipation in the NTC to 12mW, safely below the limit of 50mW specified in the datasheet.
The voltage across the thermistor can then be read by an ADC and recalculated to find the temperature. However, because the signal is very low at high temperatures, we decided to amplify it with a non-inverting op-amp circuit. We considered three requirements for the signal conditioning circuit that takes the voltage across the NTC and makes it readable by the ADC of the ATMega.
- Operate in NTC temperature range of 15C to 200C.
- Voltage must be in the range [0.5V, 4.5V]. Outside of this range, the assumption of ADC linearity is invalidated.
- The change in voltage for a 0.5K change in temperature must exceed the resolution of an 8-bit ADC with 5V reference (i.e., about 20mV)
Using these requirements, we chose four software-selectable gains for a non-inverting amplifier circuit. Without any gain, we saw that the resolution requirement is only satisfied in a narrow temperature range. We then calculated the minimum gain to meet the resolution specific for each temperature. Next, we calculated the output voltage with the minimum gain, seeing that it is in the required range for all the temperatures we need. This demonstrates a solution is possible if we can have numerous selectable gains. The next step was to choose gains for different temperature regions that meet the requirements. We chose five gain regions and tweaked them until they met spec. Finally, we calculated the value of the feedback resistors to achieve these gains, and then slightly changed the gains to produce resistor values available for purchase.
Parts List:
| PART | SOURCE | QUANTITY | UNIT COST | TOTAL COST |
|---|---|---|---|---|
| Grand Total | $60.08 | |||
| ATMega644 MCU | Lab | 1 | $6.00 | $6.00 |
| Target board | Lab | 1 | $4.00 | $4.00 |
| 12VCD power supply (1) | Lab | 1 | $5.00 | $5.00 |
| 12VCD power supply (2) | Owned | 1 | $0.00 | $0.00 |
| breadboard (small) | Lab | 2 | $1.00 | $2.00 |
| Stepper motor (Portescap 42M048C2U) | Owned | 1 | $0.00 | $0.00 |
| Quad half-bridge (TI L293DNE) | Digi-key | 1 | $2.17 | $2.17 |
| Bulk Capacitor (Kemet ESK107M025AE3AA) | Digi-key/td> | 1 | $0.18 | $0.18 |
| Resistors, diodes, and small capacitors | Lab | N/A | 0 | 0 |
| NTC Thermistor (EPCOS B57560G0103F000) | Digi-key | 1 | $3.15 | $3.15 |
| AD22100STZ Temperature sensor | Digi-key | 1 | $6.69 | $6.69 |
| Electric Burner | Amazon | 1 | $14.51 | $14.51 |
| Keypad | Lab | 1 | $6.00 | $6.00 |
| 4×20 LCD Display | Owned | 1 | $0.00 | $0.00 |
| Op-amp (MCP6231-E/P) | Digi-key | 1 | $0.38 | $0.38 |
| Header pins/sockets | Lab | 120 | $0.05 | $6.00 |
| Aluminum knitting needles | Michaels | 2 | $2.00 | $4.00 |
| Plastic collar | Scrap | 1 | $0.00 | $0.00 |
| Black Foam | Scrap | 1 | $0.00 | $0.00 |
| Foam board | Scrap | 1 | $0.00 | $0.00 |
| Aluminum C-channel | Scrap | 1 | $0.00 | $0.00 |
| 4-40 Screw | Scrap | 1 | $0.00 | $0.00 |
| Paint Stirrer | Scrap | 1 | $0.00 | $0.00 |
| Wooden table top | Scrap | 1 | $0.00 | $0.00 |
For more detail: Cooking Assistant for Automatic Temperature Control Using Atmega644